반응형
https://www.acmicpc.net/problem/9465
9465번: 스티커
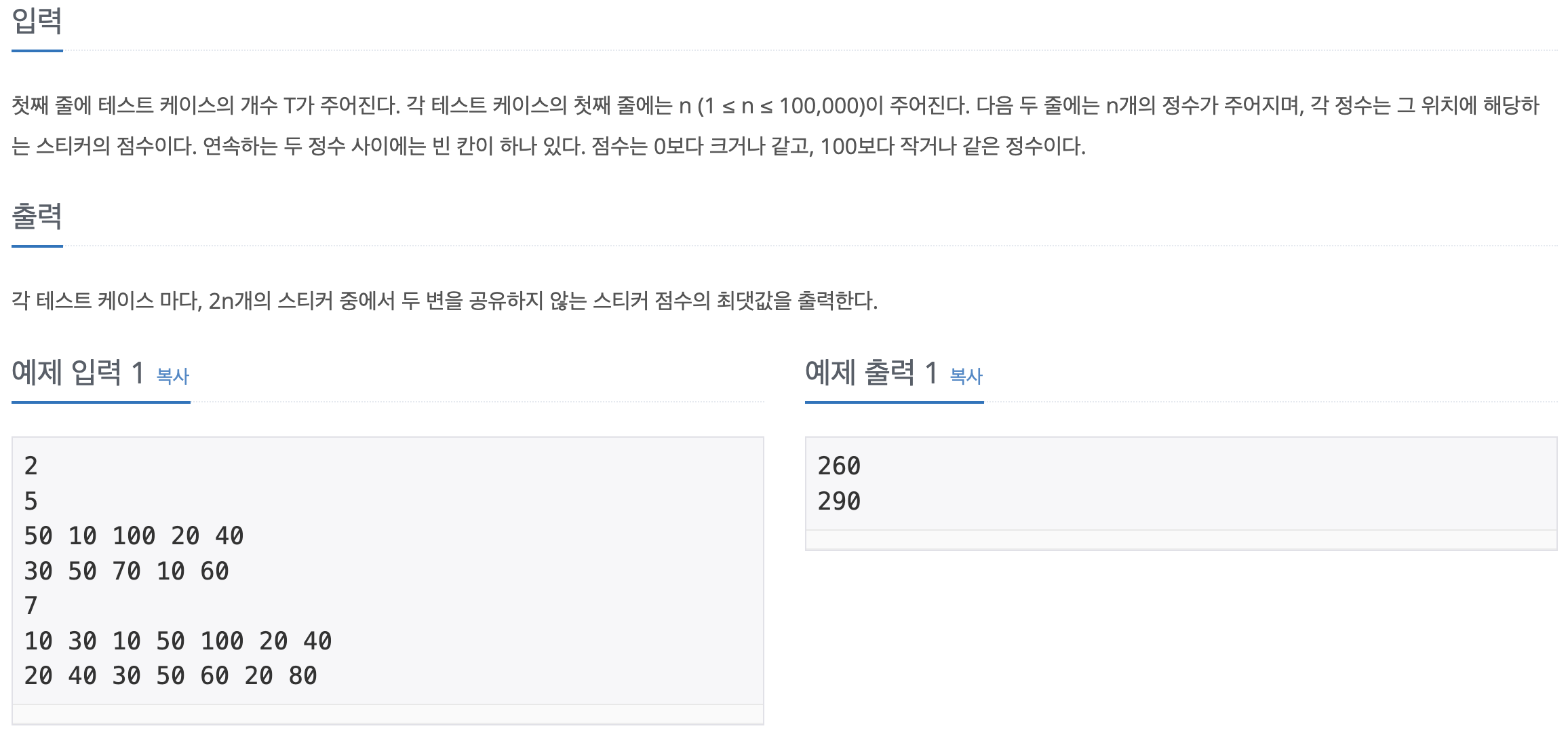
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스의 첫째 줄에는 n (1 ≤ n ≤ 100,000)이 주어진다. 다음 두 줄에는 n개의 정수가 주어지며, 각 정수는 그 위치에 해당하는 스티커의
www.acmicpc.net

[ 코드 ]
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = null;
int T = Integer.parseInt(br.readLine());
for (int tc=1; tc<=T; tc++) {
int N = Integer.parseInt(br.readLine());
int[][] sticker = new int[2][N+1];
for (int i=0; i<2; i++) {
st = new StringTokenizer(br.readLine());
for (int j=1; j<=N; j++) {
sticker[i][j] = Integer.parseInt(st.nextToken());
}
}
for(int i=2; i<=N; i++) {
sticker[0][i] += Math.max(sticker[1][i-1], sticker[1][i-2]);
sticker[1][i] += Math.max(sticker[0][i-1], sticker[0][i-2]);
}
System.out.println(Math.max(sticker[0][N], sticker[1][N]));
}
}
}
[ 실패 코드 ]
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = null;
int T = Integer.parseInt(br.readLine());
for (int tc=1; tc<=T; tc++) {
int N = Integer.parseInt(br.readLine());
int[][] sticker = new int[2][N];
for (int i=0; i<2; i++) {
st = new StringTokenizer(br.readLine());
for (int j=0; j<N; j++) {
sticker[i][j] = Integer.parseInt(st.nextToken());
}
}
for (int i=2; i<N; i+=2) {
sticker[0][i] += Math.max((sticker[0][i-2] + sticker[1][i-1]), sticker[1][i-2]);
sticker[1][i] += Math.max((sticker[1][i-2] + sticker[0][i-1]), sticker[0][i-2]);
}
System.out.println(Math.max(sticker[0][N-1], sticker[1][N-1]));
}
}
}
점화식을 세우고 결과값이 들어맞아서 너무 기뻤지만 알고보니 이것은 반쪽짜리 점화식입니다!
칸이 홀수개일때 가능한 점화식. 반쪽짜리 점화식이었다! 미리 두칸을 계산해버리는 식입니다.
1. 지그재그로 한칸씩 두개
2. 건너서 한개
둘 중 하나의 경우의 수를 체크한건데, 한번에 두 칸씩 하다보니 짝수칸일때는 계산이 안된다.
※ 오늘의 교훈
DP 문제 감이 잡혀가고, 점화식을 직접 세워가는 것만으로도 잘했다. 더 간단한 점화식을 생각해보자!
반응형
'Algorithm > 백준' 카테고리의 다른 글
| [백준] 5052번 : 전화번호 목록 / java - String, Hash 문제 (0) | 2022.05.06 |
|---|---|
| [백준] 1149번 : RGB거리 / java - DP 문제 (0) | 2022.04.13 |
| [백준] 16236번 : 아기 상어 / java (0) | 2021.08.09 |
| [백준] 2750번 : 수 정렬하기 / java (0) | 2021.04.20 |
| [백준] 14503번 : 로봇 청소기 / java (2) | 2021.02.26 |



